Poker Probability Straight Flush

- Poker Probability Straight Flush Rules
- Probability Of Straight Flush Poker
- Poker Probability Straight Flush Valve
- Poker Probability Straight Flush Video Poker
- Poker Probability Straight Flush Lines
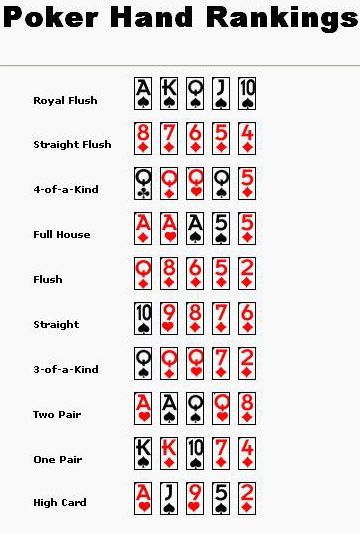
The probability of being dealt a royal flush is the number of royal flushes divided by the total number of poker hands. We now carry out the division and see that a royal flush is rare indeed. There is only a probability of 4/2,598,960 = 1/649,740 = 0.00015% of being dealt this hand. We start by finding the probability of a straight flush. A straight flush is a hand with all five cards in sequential order, all of which are of the same suit. In order to correctly calculate the probability of a straight flush, there are a few stipulations that we must make. We do not count a royal flush as a straight flush.
7 Card Poker Probabilities
for various wild card specifications
Including a “Pai Gow” (“Bug”) Joker
for various wild card specifications
Including a “Pai Gow” (“Bug”) Joker
The tables below show the probabilities of being dealt various poker hands with different wild card specifications. Each Poker hand consists of selecting the 5 best cards from a random 7 card deal.
While probabilities for the best 5 card hand from a deal of 7 cards (but no wild cards) can be calculated via direct combinatorics, the introduction of wild cards greatly complicates the combinatoric calculations. Thus, to produce the results shown here, the author wrote a computer program that would generate all possible poker hands. Each of these poker hands was evaluated for matched ranks (pairs, 3 of a kind, etc.), straights, and flushes. Wild cards introduce multiple evaluations for a given hand, and the best standard evaluation for any given hand is used in the tables.
Data from this page may be freely used provided it includes an acknowledgement to the author.
7 card poker probabilities if there are no wild cards
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 0 0.00000000
Royal straight flush 4,324 0.00003232
Other straight flush 37,260 0.00027851
4 of a kind 224,848 0.00168067
Full House 3,473,184 0.02596102
Flush 4,047,644 0.03025494
Ace high straight 747,980 0.00559093
Other straights 5,432,040 0.04060289
3 of a kind 6,461,620 0.04829870
2 pairs 31,433,400 0.23495536
One pair >= Jacks 18,188,280 0.13595201
One pair <= Tens 40,439,520 0.30227345
Ace high 12,944,820 0.09675870
King high 6,386,940 0.04774049
Queen high 2,719,500 0.02032746
Jack high 963,480 0.00720173
Ten high 248,640 0.00185851
Nine high 31,080 0.00023231
Subtotals high card only 23,294,460 0.17411920
Total = 133,784,560 1.00000000
= COMBIN(52,7)
 (Interesting observation: If a hand evaluates to just one pair, it is not distributed 4/13 “Jacks or better”. If you have a single middle-sized pair, you have a slightly increased chance of also having a straight which evaluates to a better hand. Thus a middle-sized pair occurs slightly less often than a high (Jacks or better) or a low (5’s or lower) pair.)
(Interesting observation: If a hand evaluates to just one pair, it is not distributed 4/13 “Jacks or better”. If you have a single middle-sized pair, you have a slightly increased chance of also having a straight which evaluates to a better hand. Thus a middle-sized pair occurs slightly less often than a high (Jacks or better) or a low (5’s or lower) pair.)7 card poker probabilities if one “Pai Gow” (“Bug”) Joker is added to the deck
A “Pai Gow” (“Bug”) Joker is partially wild. If you are using it to complete a straight and/or a flush, it is an ordinary wild card. If you are using it for pairs, 3-of-a-kind, etc., it is forced to be an Ace.
(Computer program and data by Bill Butler)
 Poker Hand Nbr. of Hands Probability
Poker Hand Nbr. of Hands Probability----------------------------------------------------
5 Aces 1,128 0.00000732
Royal straight flush 26,132 0.00016953
Other straight flush 184,832 0.00119909
4 of a kind 307,472 0.00199472
Full House 4,188,528 0.02717299
Flush 6,172,088 0.04004129
Ace high straight 1,554,156 0.01008255
Other straights 9,681,872 0.06281094
3 of a kind 7,470,676 0.04846585
2 pairs 35,553,816 0.23065464
One pair >= Jacks 19,273,104 0.12503386
One pair <= Tens 44,948,856 0.29160476
Ace high 14,430,780 0.09361938
King high 6,386,940 0.04143514
Queen high 2,719,500 0.01764270
Jack high 963,480 0.00625056
Ten high 248,640 0.00161305
Nine high 31,080 0.00020163
Subtotals high card only 24,780,420 0.16076246
Total = 154,143,080 1.00000000
= COMBIN(53,7)
7 card poker probabilities if one ordinary Joker is added to the deck
Poker Probability Straight Flush Rules
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 14,664 0.00009513
Royal straight flush 26,132 0.00016953
Other straight flush 184,832 0.00119909
4 of a kind 1,121,024 0.00727262
Full House 5,997,144 0.03890635
Flush 6,027,224 0.03910149
Ace high straight 1,543,460 0.01001316
Other straights 9,540,480 0.06189366
3 of a kind 13,315,300 0.08638273
2 pairs 31,433,400 0.20392352
One pair >= Jacks 21,170,640 0.13734408
One pair <= Tens 40,474,320 0.26257630
Ace high 12,944,820 0.08397925
King high 6,386,940 0.04143514
Queen high 2,719,500 0.01764270
Jack high 963,480 0.00625056
Ten high 248,640 0.00161305
Nine high 31,080 0.00020163
Subtotals high card only 23,294,460 0.15112232
Total = 154,143,080 1.00000000
= COMBIN(53,7)
7 card poker probabilities if two Jokers are added to the deck
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 88,608 0.00050033
Royal straight flush 91,764 0.00051815
Other straight flush 548,196 0.00309539
4 of a kind 3,134,544 0.01769923
Full House 8,521,104 0.04811449
Flush 8,397,324 0.04741557
Ace high straight 2,531,540 0.01429436
Other straights 14,181,120 0.08007383
3 of a kind 20,216,380 0.11415198
2 pairs 31,433,400 0.17748899
One pair >= Jacks 24,153,000 0.13638014
One pair <= Tens 40,509,120 0.22873513
Ace high 12,944,820 0.07309305
King high 6,386,940 0.03606392
Queen high 2,719,500 0.01535568
Jack high 963,480 0.00544030
Ten high 248,640 0.00140395
Nine high 31,080 0.00017549
Subtotals high card only 23,294,460 0.13153239
Total = 177,100,560 1.00000000
= COMBIN(54,7)
7 card poker probabilities with One-eyed Jacks wild
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 75,072 0.00056114
Royal straight flush 54,508 0.00040743
Other straight flush 447,946 0.00334826
4 of a kind 2,552,718 0.01908081
Full House 6,733,344 0.05032975
Flush 6,388,172 0.04774970
Ace high straight 1,404,464 0.01049795
Other straights 11,201,130 0.08372513
3 of a kind 15,758,140 0.11778743
2 pairs 23,810,436 0.17797596
One pair >= Jacks 16,255,890 0.12150797
One pair <= Tens 32,047,590 0.23954625
Ace high 9,743,580 0.07283038
King high 4,662,000 0.03484707
Queen high 1,888,110 0.01411306
Jack high 481,740 0.00360086
Ten high 248,640 0.00185851
Nine high 31,080 0.00023231
Subtotals high card only 17,055,150 0.12748220
Total = 133,784,560 1.00000000
= COMBIN(52,7)
7 card poker probabilities with Deuces (2’s) wild
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 609,760 0.00455778
Royal straight flush 399,484 0.00298602
Other straight flush 1,552,732 0.01160621
4 of a kind 7,504,920 0.05609706
Full House 9,421,824 0.07042535
Flush 7,993,600 0.05974979
Ace high straight 4,033,160 0.03014668
Other straights 15,355,640 0.11477887
3 of a kind 20,151,920 0.15062964
2 pairs 19,491,840 0.14569574
One pair >= Jacks 16,211,160 0.12117362
One pair <= Tens 20,708,880 0.15479275
Ace high 6,386,940 0.04774049
King high 2,719,500 0.02032746
Queen high 963,480 0.00720173
Jack high 248,640 0.00185851
Ten high 31,080 0.00023231
Nine high 0 0.00000000
Subtotals high card only 10,349,640 0.07736050
Total = 133,784,560 1.00000000
= COMBIN(52,7)
7 card poker probabilities with 2 Jokers,
One-eyed Jacks, and Deuces (2’s) wild
(8 out of 54 cards are wild)
(Computer program and data by Bill Butler)
Poker Hand Nbr. of Hands Probability
----------------------------------------------------
5 of a kind 5,496,072 0.03103362
Royal straight flush 1,821,704 0.01028627
Other straight flush 6,959,976 0.03929957
4 of a kind 23,628,576 0.13341898
Full House 12,751,424 0.07200104
Flush 13,497,668 0.07621471
Ace high straight 6,037,238 0.03408932
Other straights 25,527,008 0.14413849
3 of a kind 28,206,968 0.15927091
2 pairs 14,381,496 0.08120525
One pair >= Jacks 15,378,900 0.08683711
One pair <= Tens 16,024,260 0.09048114
Ace high 4,693,080 0.02649952
King high 1,911,420 0.01079285
Queen high 629,370 0.00355374
Jack high 124,320 0.00070197
Ten high 31,080 0.00017549
Nine high 0 0.00000000
Subtotals high card only 7,389,270 0.04172358
Total = 177,100,560 1.00000000
= COMBIN(54,7)
Alsoplease see 5 card Poker probabilities
Alsoplease see 6 card Poker probabilities
Probability Of Straight Flush Poker
Alsoplease see 8 card, 9 card, and 10 card Poker probabilities
Return to the main Poker probabilities page
Poker Probability Straight Flush Valve
Return to Durango Bill’s home page
Poker Probability Straight Flush Video Poker
Web page generated via Sea Monkey's Composer HTML editor
within a Linux Cinnamon Mint 18 operating system.